看完这篇弄懂统计一个关键数据：平均数，其实有感几个

这篇讲平均数

平均数是统计学的关键数据。

我们可以利用它分析数据，得出一些重要结论，来作为决策的参考。

但提到平均数，大家首先想到的是算术平均数。

其实，在统计学里平均数有好几个呢。

下面我们一一详解。

01

你以为的平均数，

有另外一个名字

当你在学校学了加法和除法，你就能计算平均数了。

大概三年级的时候，你会碰到到这样的问题。

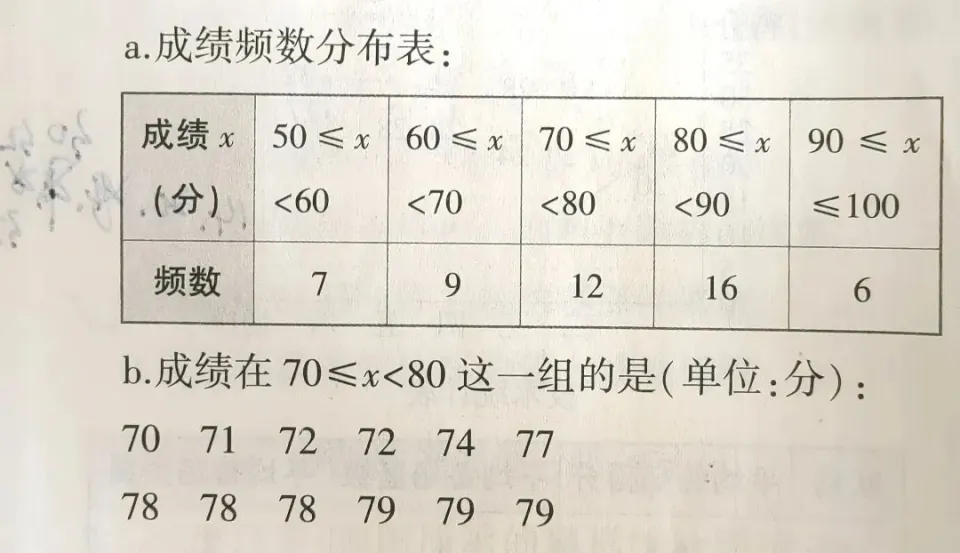
一个小组6个人，数学成绩分别是76、85、83、86、91、79，请计算这组同学的平均分？

老师会告诉你：

第一步：78+85+84+86+92+79=504

第二步：504÷6=84.

84就是平均分。

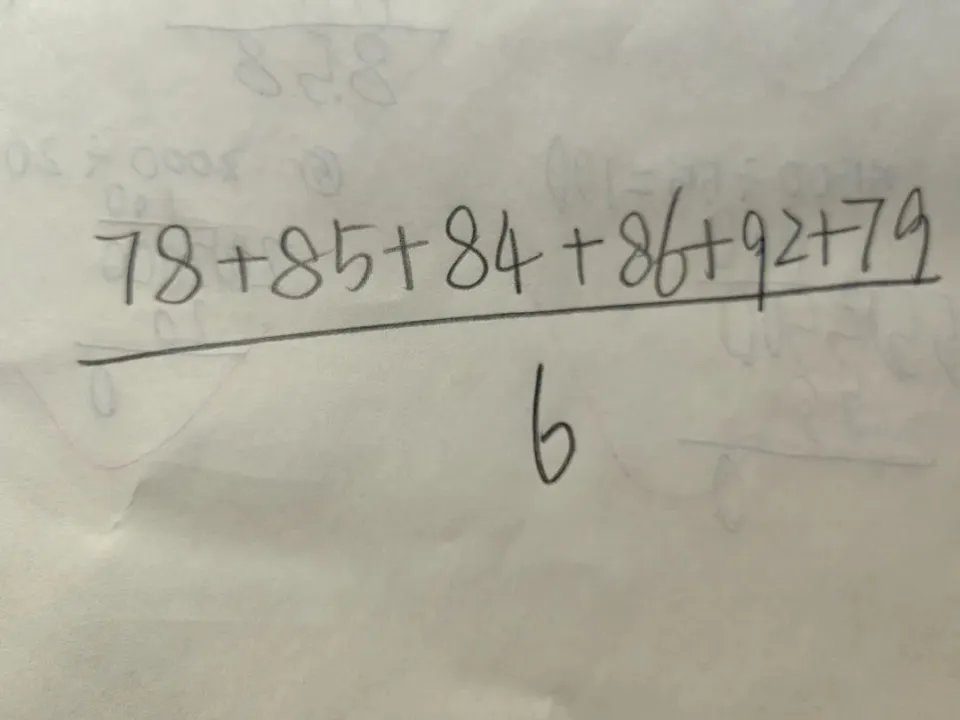
如果去掉“分”这个单位（量纲），84也叫这一组数的平均数。

这就是你以为的“平均数”——也是大多数人以为的平均数。

其实，它只是平均数的一种，在数学上有个专有名称——算术平均数。

02

算术平均数

反映了数据大小上的集中趋势

大小上的集中趋势，什么意思？

一组数，有大有小。

就比如你们班的数学成绩，有高分有低分。

现在有人问，你班数学成绩如何？

你怎么回答呢？

而一个同学说，我们班大部分学生在80分左右。

这么一来，你就知道一个班里的整体水平了。

这句话表达了两个关键点：

总结起来就是：大家都集中在80分附近。

大家都在80分附近，就是分数的集中趋势——且是“数量”（可以理解为大家都在这儿，这儿人多，数量多）上的集中趋势。

那么，再进一步，我们不要附近，要个准确值，可以吗？

可以。

当一组数差别不大时，把它们加在一起，再除以它们的个数，得到算术平均数。

比如上文中的84。

另一组的数学算术平均分是86。

84＜86

我们可以比较出哪一组整体的数学成绩更好。

如果这次是84，下次是79。

84＞79

整体集中趋势走低，成绩下降了。

我们要找找原因。

你看，把平均分具体到数值，就可以比大小，可以做参照。

与“80分附近不同”，具体到数值的分数有高低，有大有小——所以，算术平均分，是数据【大小】上的集中趋势。

现在你理解了吗？

03

当数据差别特别大时

我们用众数和中位数

10+85+84+86+79+200=544

544÷6=90.66666667≈91

一平均，我们都迈入90分俱乐部了——偏离的有点多了吧！

像这种情况，我们通常把最高分和最低分去掉，再计算算术平均数。

85+84+86+79=334

334÷4=83.5

这就是比赛中为什么要去掉最高分和最低分——保证算术平均数的准确度。

或者有极值存在，我们不要去掉最高分和最低分了，采用中位数来表示会更好。

我们把一组数，10、78、79、84、85、86、200从小到大排一排。

中间的84就是中位数。

我们把10、79、84、85、86、200，从小到大排成一排。

中间有两个数84、85，

那么84+85=169，169÷2=84.5。

84.5是中位数。

中位数，它反映了位置的集中趋势。

大家的位置如何、“段位”如何，在这里可以看出来——中位数一出来，你离中位数多远，自己心里就有谱了。

有同学告诉大家“我们班数学成绩的中位数是84.5”，这就说明：

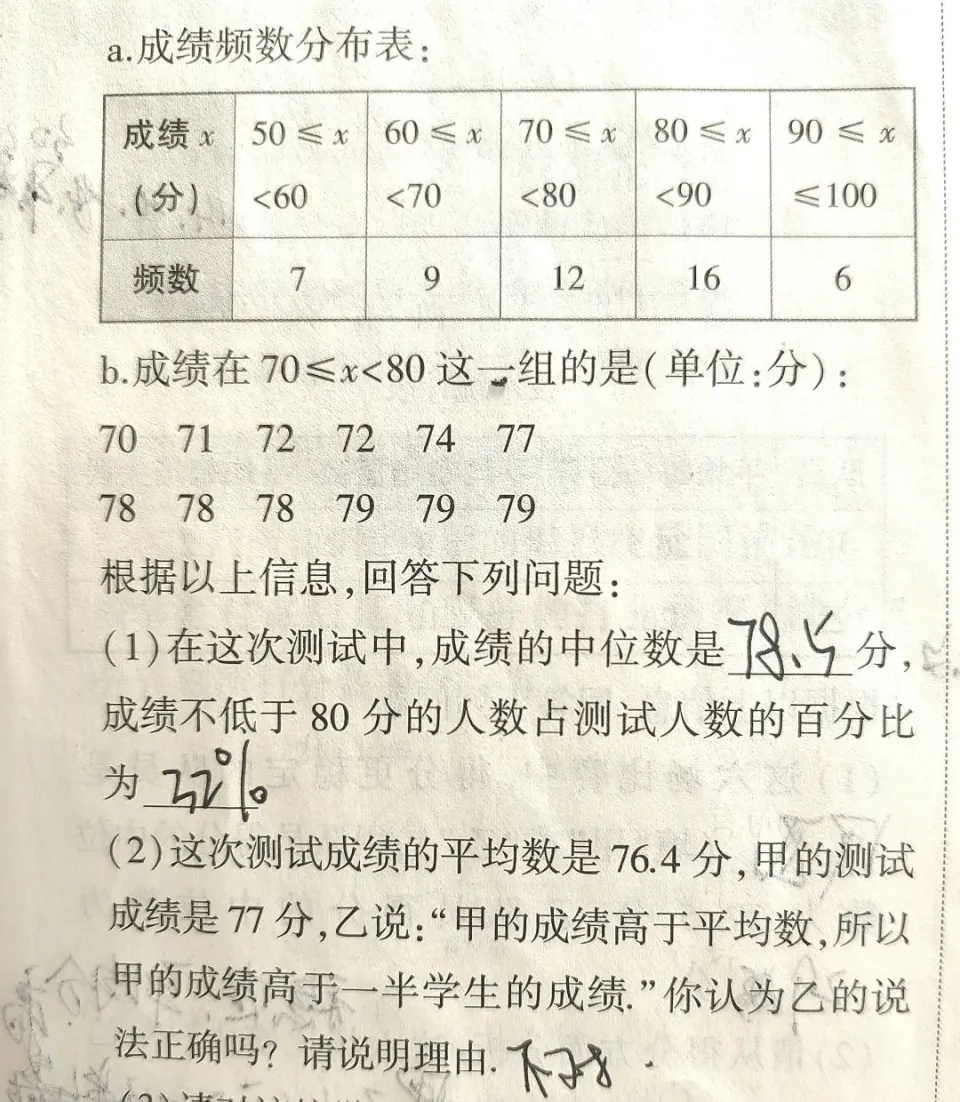
在上面这道题中，第二问就换一种方法问：位置。

中位数是78.5，考到77分，超过了平均分，并不能说明这位同学超过了一半的同学。如果他考了79，就可以这么说了。

在考试中这是一个坑，在实际应用中，中位数可以看出一个人的位置。

平常看新闻，一说收入平均数，好多人生气，我没有那么多收入……因为收入有极值。

用中位数嘛，我国收入的中位数是多少，让大家自己去衡量位置。

超过中位数——你超过了国家的一般人，超过中位数很多，你是不是有优越感？

你看，中位数也是一种平均数，适合有极值的情形。

有时候，它还和算术平均数一起使用。

比如下面这道题。

选一家快递公司应该选甲还是选乙？

这就是在考察你会不会计算平均值、知不知道它们都是平均数、是数据的重要考量。

单看数据，我们知道要用乙，因为它的平均数和中位数都大于甲，无论是大小的集中趋势还是位置的集中趋势都优于甲。

通常在题目中还有方差的考察。

从方差的计算方式就可以看出它衡量变动，衡量一组数据离平均值的远近。

如果方差大：

就像考试，你一会儿30，一会儿100，班里如果有竞赛，不能派你去，波动太大了，不稳。

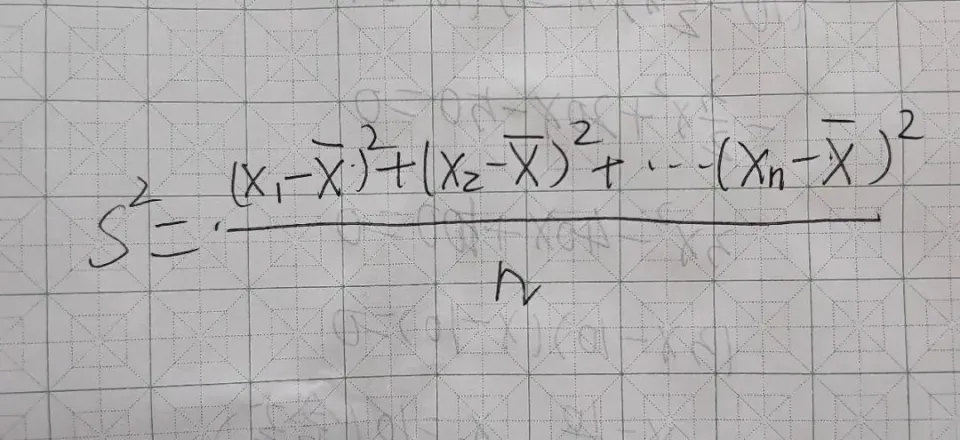
另外还有一种平均数叫众数，也适合有极值的情形。

比如，统计跳绳数量，看下表。

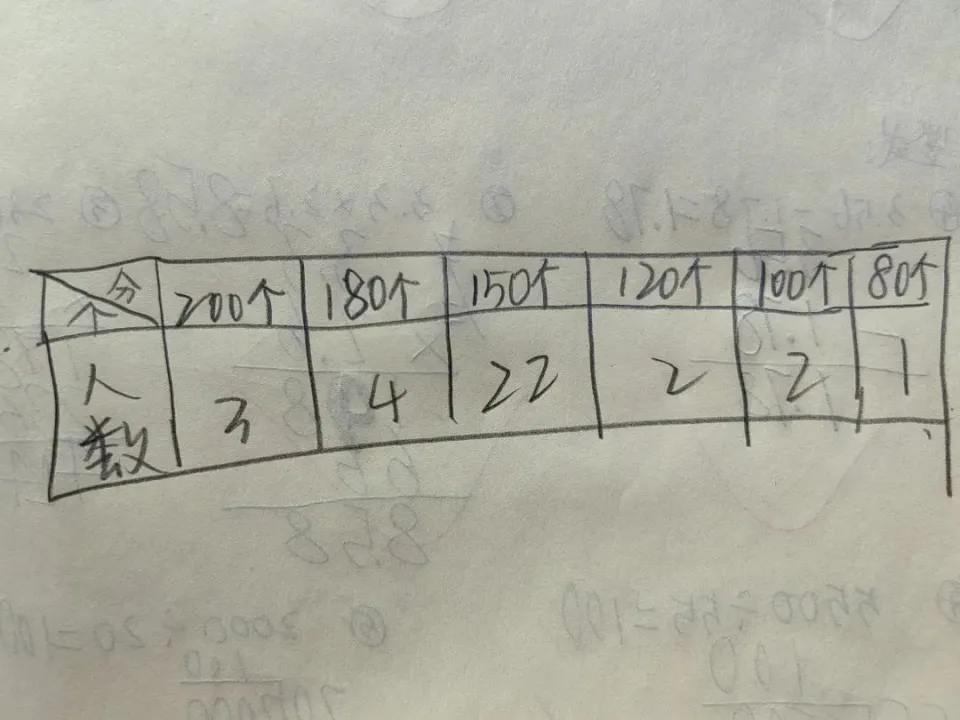
在这个表里，150个就是个众数——大部分人都在这儿。

它反映了数量上的集中趋势——大部分都集中在这儿。

在上面分数的例子里，【80附近】是个分数段，这个分数段，有更多的同学。它也是众数。

众数反映了数量的集中趋势。

它跟中位数一样，对极值也不敏感。

那么，它跟中位数的区别是啥呢？

应用的场景不同：

中位数说到底还是表示整体数据的走向——收入中位数、分数中位数；

而众数体现了群体中的多数——多数人的喜好，多数人的成绩。

这些数据，在针对某群人的时候，很有说服力。

你看，其实众数、算术平均数、中位数都是平均数，只是叫法不同，也分别适用于不同的情形。

具体如何操作，那就过于复杂了，在数据统计中不止我们说的这么简单。

但在初中和高中阶段，不是特别难。

如今，你知道的这些知识就能应对中考题了。

不信你看看。

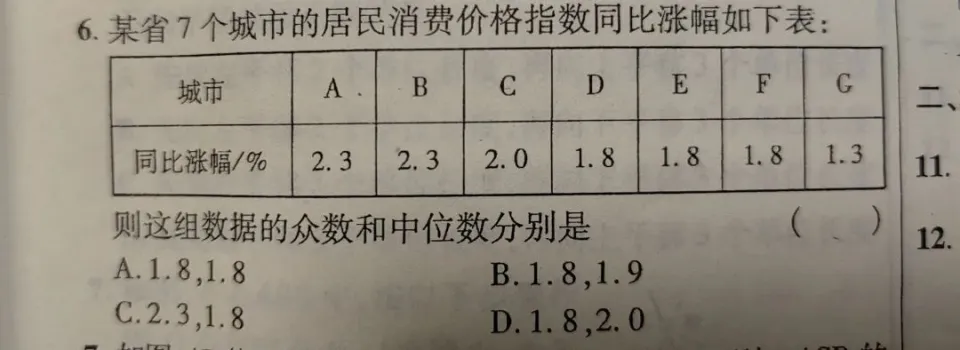
另外，题目不难，咱也得重视。

在实际应用中，生活中，你懂这几个数之间的差别，能在谈话中提及这些数，放心，你已经超越好多人了。