背包问题的贪心算法与动态规划解析

01背包问题与贪心算法

背包问题，本质上是一个关于容器容量与物品装载的优化问题。若仅考虑物品的重量，而不考虑其价值，该问题可简单地通过贪心算法来解决。例如，当有一艘船的装载量为W，需要装载N个物品，且每个物品的重量已知时，为了最大化装载数量，应优先选择重量较小的物品进行装载，直至达到装载量上限。

然而，当考虑每个物品的价值时，问题变得更为复杂。为了装载价值最大的物品，我们需要在满足装载量限制的前提下，尽可能选择单位价值最高的物品。这同样可以通过贪心算法来解决，只要确保所选物品的单位价值（即价值与重量的比值）最大且不超过最大装载量即可。

值得注意的是，贪心算法虽然能够解决某些背包问题，但它仅仅考虑了局部最优解，而并未从全局角度进行优化。因此，在处理不可分割的背包问题时，贪心算法可能无法得到最优解。为了解决这类问题，我们需要采用更为复杂的算法，如动态规划等。

动态规划在背包问题中的应用

动态规划是一种通过保存子问题的解决结果来避免重复计算，从而提升效率的算法。这种方法非常适合用于背包问题，因为它允许我们逐步构建解决方案，并通过记录每个子问题的最优解来寻找全局最优解。

动态规划的实现步骤

在背包问题中，我们使用二维数组记录每个子问题的最优解。具体来说，在面对第i件物品时，我们记录下不同的背包容量j下的最大价值。通过定义适当的状态转移方程，我们可以更新这个二维数组，以确保每一步都得到一个更优的解。

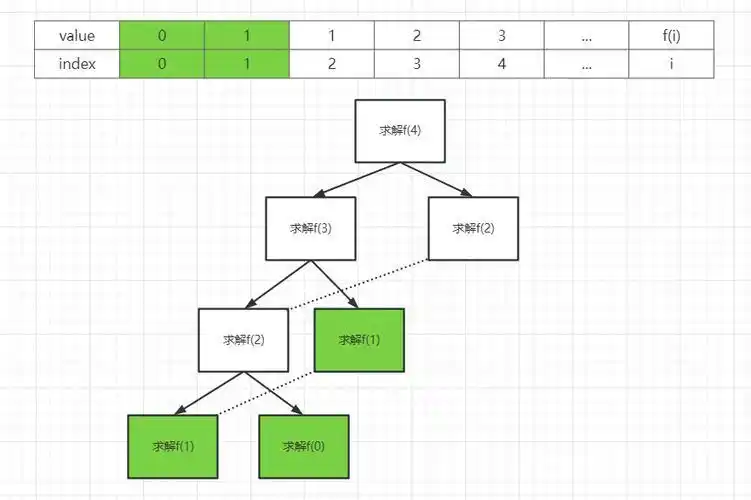
具体案例分析

接下来，我们将通过一个具体的例子来说明动态规划在背包问题中的应用。考虑到某些背包问题通过贪心算法无法达到最优解，我们需要详细分析如何通过动态规划逐步构建并填充状态表格，从而寻找背包问题的最优解。

通过上述逐步比较的方法，我们可以逐步构建出v

的完整取值规律，从而得到最优的物品放置方案。在每个空间j中，我们都会重复这样的比较和选择过程，以确定能够产生最大价值的物品放置方案。

在解决背包问题的过程中，我们通过动态规划逐步填充二维数组v来找到最优解。最终，当数组填写完毕时，我们就能找到使得背包内物品总价值最大的解决方案。