假设goods为一个包含物品信息的二维列表，其中每个子列表包含物品的重量和价值

01背包问题的动态规划解决方案

背包问题概述

从01背包问题谈起，我们深入探讨动态规划的应用。想象一下，你面前有这样几件物品：手机，重量1单位，价值5000；游戏机，重量3单位，价值7000；还有电脑，重量4单位，价值10000。然而，你只有一个容量为5单位的背包。问题来了，该如何选择，才能让背包内的物品价值最大化呢？

这个选择问题涉及多个物品的组合选择，在有限重量下选出最大价值。我们首先尝试最直观的方法——穷举（或称蛮力法）。这种方法的核心思想就是列出所有可能的情况，然后从中挑选出最优解。确实，这种方法能确保我们找到最优解，因为我们已经审视了所有选项。接下来，我们一一列举出所有可能的组合情况：

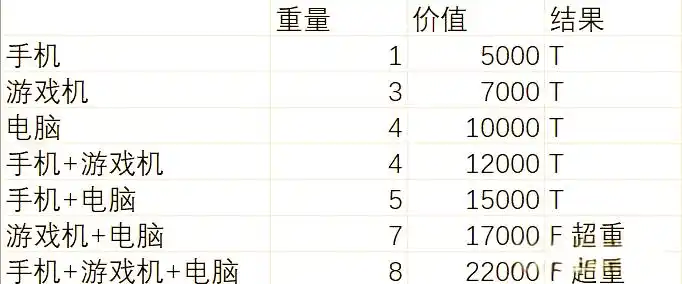
在背包恰好装满的情况下，选择“手机+电脑”的组合将能够获得最大价值，即15000元。这是通过精心规划和优化，充分利用了背包的最大重量限制和现有物品的重量与价值，从而实现了价值的最大化。

贪心算法的应用

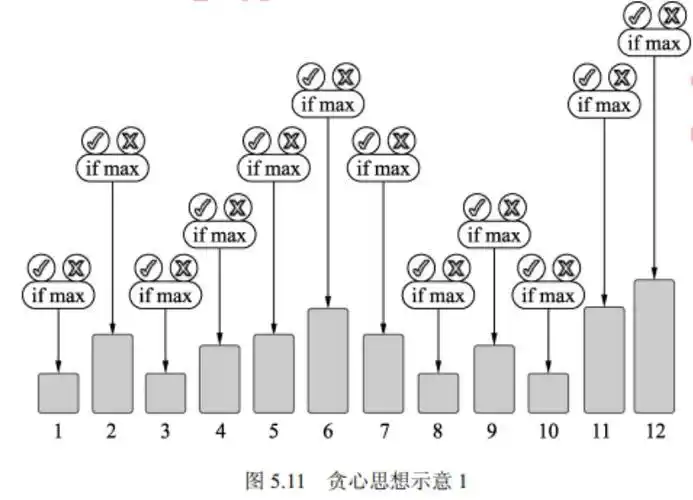
在解决背包问题时，除了穷举法，我们还探讨了几种常见的贪心策略。这些策略虽然在某些情况下能够工作，但它们的实际局限性也不容忽视。

价值贪婪：每次选取价值最高的物品。这种方法虽然单纯，但通常难以发现最优解。

重量贪婪：每次选取重量最轻的物品。这样的策略会导致更明显的低效。

价值密度贪婪：通过计算每个物品的单位价值来选择，这种方法在此问题中的应用也并非总能如愿。

贪心算法的优势在于简单直观，但其缺陷在于算法效率与问题规模之间的关系，在物品数量较多时，其计算复杂度会显著增加，导致效率低下。因此，这种简单的方法并不总是最佳选择。

动态规划方法介绍

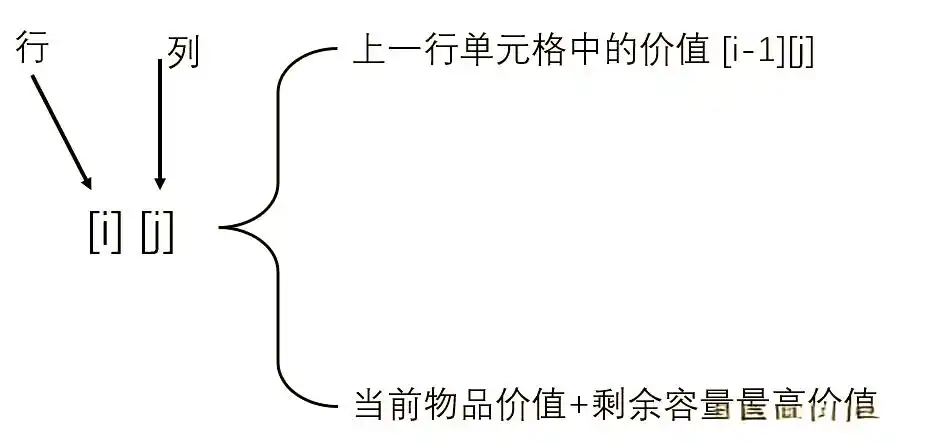
动态规划的核心思想在于通过解决一系列小问题，逐步构建出对大问题的解决方案。它通常从小规模的情况出发，通过建立一个表格结构，展示逐步构建最优解的过程，重点在于利用递归与重叠子问题的特性。对于背包问题，我们通常会构建一个表格，其中每一行代表一种物品，每一列则代表背包的不同容量。通过填充这个表格，我们可以找到使得背包总价值最大的物品组合。

例如，可以通过以下步骤进行动态规划的求解：

创建一个二维表格，每一行代表一个物品，每一列代表一个背包容量。

填充这个表格的过程中，我们不断地更新每个单元格的值，该值表示在给定容量下能达到的最大价值。

通过递推的方法，最终在表格的最后一行最后一列中找到最大值，该值即为背包的最大价值。

这种充分利用问题的重叠子问题特性，逐一构建整体最优解的方法，使得动态规划在解决背包问题时显得尤为有效。

Python实现示例

以下是一个展示动态规划算法的Python实现代码，帮助理解动态规划的表格填充方法：

```python

假设goods为一个包含物品信息的二维列表，其中每个子列表包含物品的重量和价值

goods =

bagMaxWeight_CONST = 5 # 背包最大重量

生成一个二维列表来存储动态规划表

dp_table =

for row in range(len(goods)):

colTable =

for col in range(bagMaxWeight\_CONST):